Criptografía de Curva Elíptica

La criptografía consiste en todas aquellas técnicas que permiten transformar un mensaje para evitar que receptores no autorizados puedan tener acceso a la información de dicho mensaje.

Existe una gran cantidad de técnicas que permiten ocultar la información de un mensaje, pero hay dos esquemas básicos sobre los que se construyen todos los procesos o técnicas de criptografía. Estos dos esquemas se basan en la forma en la que se comparte la clave utilizada para encriptar el mensaje:

• Métodos simétricos, en los que el emisor que encripta el mensaje y el receptor que debe desencriptar el mensaje, comparte la clave de encriptado.

• Métodos asimétricos, en los que emisor y receptor no comparten la clave de encriptado.

Los métodos de encriptación asimétricos son más seguros ya que evitan compartir la clave de encriptado, que es uno de los principales riesgos en el mundo de la criptografía, que un tercero no autorizado tenga acceso a la clave de encriptación del mensaje.

La fortaleza de los métodos asimétricos está en que se basan en problemas matemáticos que son fáciles de resolver conociendo ciertos parámetros, pero tremendamente costosos de resolver si no se conocen los parámetros importantes.

Aunque los métodos asimétricos son a priori más seguros, ya que no es necesario comunicar la clave de encriptado del mensaje, tienen dos problemas:

• Que matemáticamente se encuentre una forma de resolver el problema que hasta ahora no se conocía, lo que invalidará automáticamente este método para utilizarlos en este tipo de procesos de encriptación.

• Que la capacidad de computación va aumentando año tras año, y lo que hace un siglo, parecía un trabajo enorme,hoy en día lo puede resolver un ordenador personal. Y en concreto, la aparición de la computación cuántica, que permitiría resolver estos métodos con costes bajos de computación.

Los dos métodos de criptografía asimétrica más populares actualmente, cada uno basado en un problema distinto, pero que se están utilizando ampliamente en el mundo de las comunicaciones y las aplicaciones de internet, son RSA y Curva elíptica.

RSA basa su fortaleza en el problema de la factorización de grandes números y Curva elíptica en el problema del logaritmo discreto.

Encriptación asimétrica: Método RSA

Sin entrar en demasiada profundidad, vamos a ver de manera muy somera, en qué consiste el método de encriptación asimétrica RSA.

Este método fue desarrollado por Rivest, Shamir y Adleman, de aquí viene su nombre y se basa en la complejidad que existe para factorizar números muy grandes. Este problema de factorización de grandes números no tiene actualmente una solución eficiente, lo que lo hace especialmente interesante para desarrollar un método criptográfico asimétrico como RSA.

De forma muy esquemática, vamos a describir el método RSA:

• Se eligen dos número primos, con los que obtendremos un tercer número que es el producto de ambos:

N = p · q

• Se elige un número al que denominaremos e, el cual es un primo relativo de:

(p – 1)(q – 1)

Para elegir un primo relativo del producto anterior, tenemos que elegir un número e tal que no tenga ningún factor primo en común, es decir que su máximo común divisor sea igual a 1.

• Calculamos el número d para que cumpla:

ed = 1 mod (p – 1)(q – 1)

• La clave pública como el par (N,e)

• La clave privada es d

d = (1 mod (p – 1)(q – 1) )  / e

El proceso de cifrado de un mensaje consiste en elevar el mensaje al número e, que se denomina exponente de cifrado y calcular el módulo N.

Mensaje Cifrado = (Mensaje)e mod N

Para descifrar el mensaje cifrado sólo tendremos que utilizar N que es parte de la clave pública y d que es la clave privada.

Mensaje = (Mensaje Cifrado)d mod N

Como se puede ver, para que emisor y receptor puedan intercambiar un mensaje de manera segura, no es necesario intercambiar la clave, lo que garantiza que si un tercer usuario intercepta el mensaje tendría:

• El mensaje cifrado,
• La clave pública (N,e) del receptor, que ha utilizado el emisor para cifrar el mensaje y que es pública.

Pero no tendría acceso a la d, que es la clave privada del receptor, la cuál es necesaria para el proceso de desencriptado. Como vemos la complejidad para el atacante sería, conociendo N, encontrar p y q, que es sencillo para números pequeños, pero es muy complejo y costoso para número grandes. Hay que tener en cuenta, que RSA trabaja con números de 2048 bits, que son suficientemente grandes para considerar RSA seguro.

Encriptación asimétrica: Método Curva Elíptica

Otro método de encriptación asimétrica es el conocido como método de Curva Elíptica o ECC (Elliptic-curve cryptography).

Estos métodos tienen una ventaja sobre RSA y es que son algo más rápidos y necesitan números más pequeños para conseguir la misma fortaleza. Estos dos factores, la velocidad y el tamaño, han sido determinantes para que se utilicen de manera masiva en tecnologías Blockchain, la firma digital de las operaciones.

Los métodos basados en curvas elípticas tienen su fortaleza en que por ahora no existen técnicas computacionales eficientes que permitan resolver el logaritmo elíptico. Pero como todos los métodos de criptografía asimétrica, podrían romperse con computación cuántica, ya que se podría encontrar una forma rápida y eficiente de resolver el logaritmo elíptico. El método utiliza una curva elíptica de la forma:

y² = x³ + ax + b

El primer paso es elegir una de las curvas del dominio, para ello todas las partes que participan en el protocolo de encriptación/desencriptación del mensaje, deben establecer un consenso para elegir la curva. La realidad es que este proceso de ponerse de acuerdo sobre la curva, está limitado a un conjunto concreto de curvas, ya que son curvas probadas y que se consideran seguras.

Se denominan parámetros del dominio de la curva, a un conjunto de parámetros que se utilizan para definir una curva elíptica. Estos parámetros se deben elegir con especial cuidado ya que no todas las curvas poseen la misma fortaleza, por lo que es recomendable utilizar curvas con parámetros de dominios que ya estén validados.

La relación entre los componentes criptográficos y los elementos de la curva está representada en la siguiente ecuación, que es la base sobre la que se construye la criptografía de curva elíptica:

P = k*G

Donde P y G son puntos de la curva, y k es un entero que define el número de iteraciones que se van a realizar sobre el punto G para obtener el punto P.

Las curvas parten de un punto base denominado G y cada una tiene el suyo. Este punto es el mismo para todos los usuarios que utilicen la curva y por tanto, lo podemos considerar como un dato público. El emisor del mensaje elige un número k que será su clave privada, este número no puede ser revelado a nadie, ya que es el único dato que debe permanecer en secreto. El punto P es la clave pública y se genera a partir de la clave privada k.

• Clave privada:  k 

• Clave pública: P = k*G

Sin entrar a explicar las matemáticas detrás de la criptografía basada en curvas elípticas, para lo que recomiendo el libro “Criptografía con curvas elípticas” de Victor Gayoso, Luis Hernández y Agustón Martín, solo mencionar algunos conceptos para entender un poco mejor la naturaleza de los cuerpos de números con los que trabajan las curvas: 

• Se trabaja sobre cuerpos finitos F_q donde q =p^m y p es un número primo.
• El orden de un cuerpo finito es el número de elementos de dicho cuerpo.
• El orden de la curva es el número de puntos que pertenecen a dicha curva.
• El orden de un punto P es el número entero más pequeño que cumple que nP = O
• Al ser cuerpos finitos, todas las operaciones (suma o multiplicación) se realizan con módulo.

¿Esto qué quiere decir? Pues básicamente, que en criptografía de curva elíptica:

• Se emplea una función que define la curva, existen distintas curvas y por lo tanto distintas funciones, pero todas se basan en la siguiente fórmula. 

y² = x³ + ax + b

• Se trabaja con un cuerpo finito de elementos los cuales pertenecen a la curva.

• Los elementos del cuerpo se generan desde un punto de la curva, que se denomina generador. Esto también es importante tenerlo en cuenta, ya que para una misma curva, podemos tener distintos puntos Generadores, lo que significa que tendríamos distintos cuerpos de elementos. 

• Todos los puntos con los que vamos a trabajar, estarán generados por el mismo punto y se generan en base a iteraciones sobre ese punto Generador.

¿Cómo se genera el cuerpo de elementos con lo que trabajaremos?

Hay un método denominado “la cuerda y la tangente” con el que podemos realizar la operación de suma de dos puntos de la curva. Tenemos 2 puntos de la curva a los que llamaremos P y Q, la operación de suma consiste en trazar la recta que pasa por ambos puntos. Esta recta corta a la curva en un punto R, el simétrico de dicho punto se considera (P + Q)

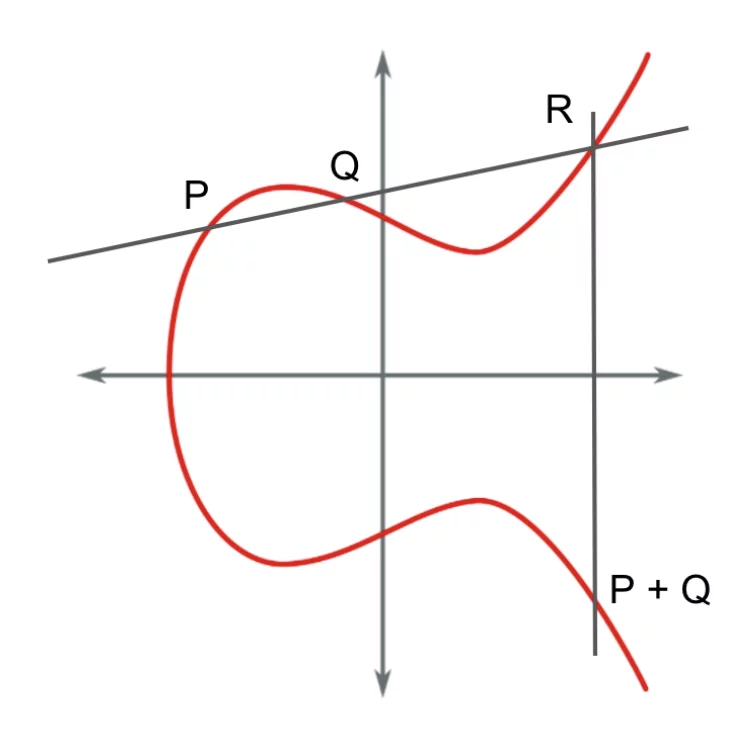
Obtenemos un nuevo  punto de la curva N = P + Q

Ahora supongamos que solo tenemos un punto P, el cual sumamos con el mismo (P + P), como recta de corte se utiliza la tangente de la curva en el punto P.

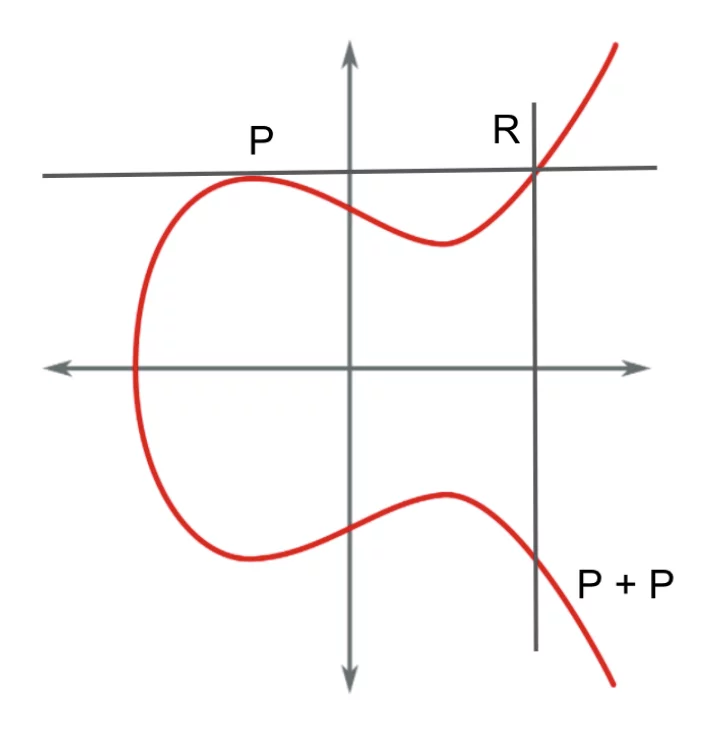
En este caso N = P + P = 2P, por tanto si multiplicamos el punto P un número x de veces, obtenemos un nuevo punto N’ de la curva. Disponemos de dos operaciones:

• Suma de puntos definidas en la curva elíptica forma un grupo abeliano porque cumple con:
  • Conmutativa: P + Q = Q + P
  • Elemento inverso: P + Q = O, donde Q = – P
  • Elemento Neutro: P + O = P
  • Asociativa: (P1 + P2) + P3 = P1 + (P2 + P3)

• Multiplicación escalar de un número por un punto de la curva.
  • N = 2P = P + P
  • N₄ = 4P =  P + 3P = P + P + 2P = P + P + P + P 

Con este método podemos generar el cuerpo de elementos pertenecientes a la curva y que han sido generados con el punto Generador. La siguiente serie muestra cómo se calcularán todos los puntos de la curva en base al generador G:

• P₀ = G
• P₁ = G + P_o = 2G
• P₂ = G + P₁ = 3G
• P₃ = G + P₂ = 4G
• …
• P_n-1 = G + P_n-2 = nG

Ya tenemos definido el cuerpo de elementos, entonces para cualquier punto del cuerpo podemos decir que se puede calcular multiplicando un número entero por el punto Generador.

P = k*G

Antes hemos comentado que cada uno de estos componentes, los asociamos a un  elemento criptográfico

• G es el punto base o generador, que es conocido por todo el mundo y único para la curva que estamos utilizando, es decir, si dos usuarios utilizan distintos puntos base, están empleando distintos cuerpos de puntos, lo que haría imposible que se puedan entender.

• k es la clave privada que mantendremos en secreto. Es un número que define la veces que hay que iterar sobre G.  

• P es la clave pública y consiste en un punto que ha sido generado iterando k veces sobre G, este punto es público y se puede compartir con otros usuarios, de hecho es necesario compartirlo para que este método asimétrico funcione.

El problema a resolver

Como no hemos profundizado en las matemáticas de curva elíptica, podrás pensar que ¿dónde está la complejidad de todo esto? Si P y G son públicos, podrías conocer k haciendo la siguiente operación.

P = k*G

k=P/G

La respuesta es que el cuerpo de elementos con los que trabajan las curvas elípticas permiten la suma de dos puntos y la multiplicación escalar de un número y un Punto, pero no se pueden dividir dos puntos, esto significa que no podemos calcular k intentando dividir el punto P entre el punto G. Emplear curvas elípticas para la encriptación tiene como fortaleza principal, la dificultad actual que existe para resolver el problema del logaritmo discreto sobre curvas elípticas (ECDLP) que es el siguiente:

Dado una curva elíptica E definida sobre un cuerpo finito Fq, un punto P ∈ E(Fq) de orden n y un punto Q ∈ hPi, encontrar el entero k ∈ [0, n − 1] tal que Q = kP. El entero k se llama el logaritmo discreto de Q respecto a la base P y se denota k = log_p Q.

No existe una manera de resolver este problema, más allá de la fuerza bruta. Para atacar este problema por fuerza bruta supongamos que elegimos un número k de tamaño 256 bits, eso significa que el atacante debe realizar 2^256 operaciones de suma sobre el punto G, hasta encontrar el punto P, en ese momento habría encontrado el número k es es la clave privada. 

P = k*G

Pero hagamos algunas estimaciones, por ejemplo:

• Supongamos que de promedio el atacante ejecuta solo la mitad de las operaciones de suma hasta encontrar k, es decir, el atacante debería realizar 2¹²⁸ sumas.
• Aventuremos que el atacante tiene una capacidad de cómputo que le permite realizar 1 millón de sumas por segundo, es decir, es capaz de realizar unas 2²⁰ operaciones por segundo.
• Un año tiene unos 2²⁵ segundos.
• Por tanto, en un año podrá hacer  2²⁰ x 2²⁵ = 2⁴⁵ sumas.
• Necesitaría 30.000.000.000.000.000 millones de años para realizar 2¹²⁸ sumas, teniendo en cuenta que la edad del universo es de 14.000 millones de años, la probabilidad de encontrar k por fuerza bruta son mínimas.

Pero entonces ¿Cómo se calcula P?

Si aún no te has perdido, te estarás preguntando que si tan costoso es encontrar k, y que P es un punto que se calcula iterando k veces sobre G, ¿cuánto tiempo tardaremos en calcular P dado un k de tamaño 2²⁵⁶?, ya que la única forma de calcular P es internado k veces sobre G. Si tenemos que k = 354 (es un número relativamente pequeño), habría que hacer el siguiente conjunto de iteraciones con operaciones de suma sobre G, para obtener P:

• P₀ = G
• P₁ = G + P_o = 2G
• P₂ = G + P₁ = 3G
• P₃ = G + P₂ = 4G
• …
• P₃₅₃ = G + P₃₅₂ = 354G

Pero este método de obtener P sería inviable, ya que para valores de k del orden de 2²⁵⁶ se tardarían miles y millones de años, igual que ocurre al intentar atacar por fuerza bruta el problema del logaritmo discreto de curva elíptica. Para ahorrar tiempo a la hora de calcular P, se utiliza un método que solo requieres de 256 operaciones, en el caso de que k tenga ese tamaño de bits. Supongamos que k=356, el método es el siguiente:

• Se calcula la serie, utilizando el elemento anterior:
  • 2⁰G = G
  • 2¹G = 2⁰G + 2⁰G = G + G
  • 2²G = 2¹G + 2¹G = 2G + 2G 
  • 2³G = 2²G + 2²G = 4G + 4 G
  • 2⁴G = 2³G + 2³G = 8G + 8G
  • 2⁵G = 2⁴G + 2⁴G = 16G + 16G
  • …
  • 2²⁵⁵G = 2²⁵⁴G + 2²⁵⁴G 

• Pasamos k a binario y se convierte en una suma de potencias:
  • 0101100100
  • 2⁸+2⁶+2⁵+2² = 356

• Se construye la suma de los términos necesarios
  • P = 2⁸G+2⁶G+2⁵G+2²G = 356G

De esta forma, se puede calcular P de manera sencilla y rápida, sin la necesidad de iterar sobre G las k veces necesarias y aquí radica la potencia de las curvas elípticas en criptografía, que podemos hacer ciertas operaciones con muy poco coste de tiempo, pero realizar las operaciones inversas tienen un coste demasiado elevado para considerarlas. 

Diffie-Hellman con Curva elíptica

Se denomina Diffie-Hellman al protocolo que permite establecer un clave de encriptación/desencriptación sin la necesidad de intercambiar la clave entre emisor y receptor. La criptografía de curva elíptica permite implementar un protocolo de Diffie-Hellman sencillo para compartir una clave simétrica de encriptación del dato. El proceso sería el siguiente:

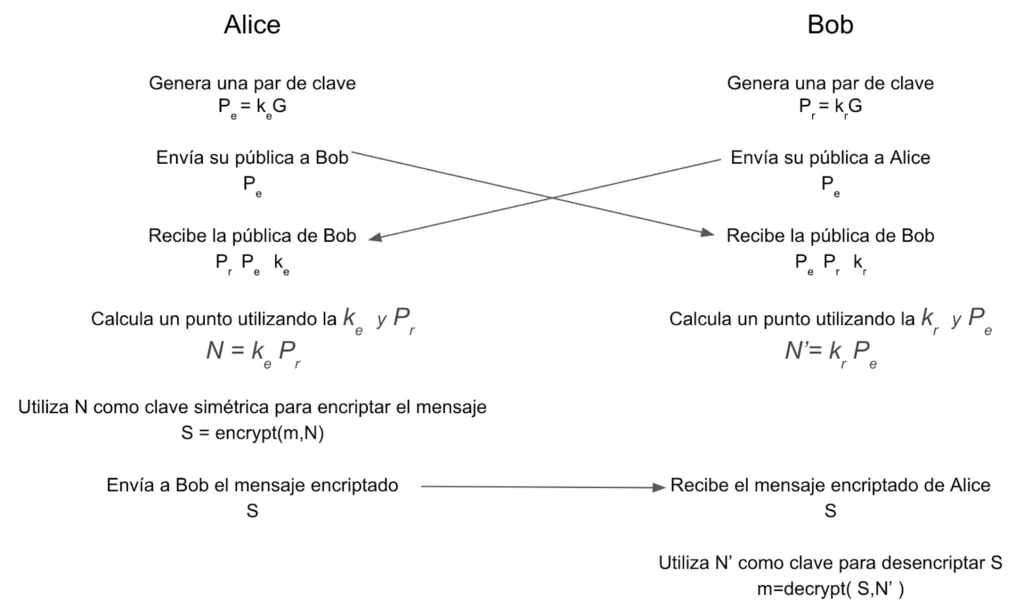
A continuación se detallan los pasos descritos en el diagrama anterior:

• El emisor y receptor eligen un punto G, normalmente este punto ya está establecido para una curva en concreto.

• El emisor elige un número que debe permanecer en secreto y que será su clave privada, a este número lo llamaremos k_e.

• El emisor genera su clave pública de la siguiente forma

P_e = k_eG

Recordemos que la operación de multiplicación k_eG consiste en iterar k_e veces el punto G para obtener un nuevo punto P que será la clave pública.

• El receptor elige un número que debe permanecer en secreto y que será su clave privada, a este número lo llamaremos k_r.

• El receptor genera su clave pública de la siguiente forma

P_r = k_rG

• Ambos intercambian sus respectivas claves públicas.

• Emisor recibe la clave pública P_r
• Receptor recibe la clave pública P_e

• Si el emisor multiplica su k_e  por la clave pública del receptor P_r, obtendrá un nuevo punto de la curva al que denominaremos N.

N = k_e P_r 

• Si el receptor multiplica su k_r  por la clave pública del emisor P_e, obtendrá un nuevo punto de la curva que denominaremos N’.

N’ = k_r P_e 

Podemos demostrar matemáticamente, que N y N’ son el mismo punto de la curva, de la siguiente forma:

N = N´

k_e P_r  = k_r P_e 

k_e k_rG = k_r k_eG 

Como se ve en el desarrollo anterior, sin necesidad de intercambiar las claves privadas, tanto receptor como emisor, son capaces de ponerse de acuerdo en elegir la misma clave para encriptar el mensaje.Si un tercer usuario intercepta el mensaje cifrado, al no tener acceso a k_r o k_e, no podrá descifrar el mensaje.

Firma digital con curva elíptica o ECDSA

Una de las propiedades de la criptografía asimétrica es la capacidad para firmar digitalmente algo y demostrar el origen de la firma digital. Por ejemplo, Alice quiere enviar un mensaje a Bob, pero necesita asegurar que el mensaje que recibe Bob es el mismo que el que ella ha enviado. Para asegurar la integridad del mensaje Alice va a firmar digitalmente el mensaje y Bob podrá verificar la firma digital del mensaje y comprobar que la identidad digital del firmante coincide con la de Alice.

El siguiente diagrama muestra el esquema del flujo y las acciones entre Alice y Bob.

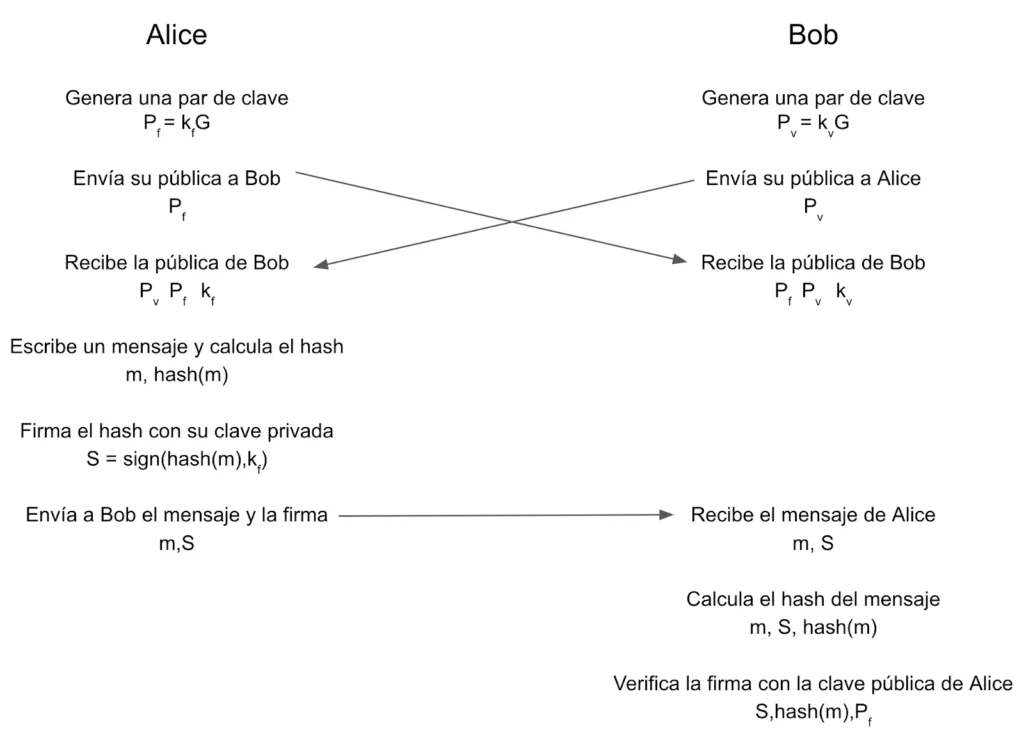
Algoritmo para firmar

Este es el algoritmo que se emplea para implementar la firma digital utilizando curva elíptica. Los datos de entrada necesarios son:

• El mensaje m
• La clave privada del firmante k_f

Se ejecutan estos pasos:

1. El firmante calcula el hash del mensaje.
   • H(m)
2. El firmante calcula r
   • Se genera un número aleatorio k
   • Se calcula el punto N = kG = (x,y)
   • Se calcula r, donde n es el orden de la curva.
     • r = x(mod n) 
3. El firmante calcula s:
   • s = k^-1 (H(m) + k_f r )  (mod n)
4. La firma del mensaje m es el par (r,s)

Como estamos trabajando con grupos finitos, las operaciones se realizan con módulo de n, donde n es el orden de la curva, recuerda que el orden de la curva es el número de puntos de la curva.

En este punto, tenemos los siguientes elementos:

• P = k_f G la clave pública y privada
• H(m) el hash del mensaje
• N = kG un punto que hemos generado con un número aleatorio
• r = Nx(mod n) calculamos el módulo n de la componte X del punto N
• s que hemos calculado para relacionar k,k_f ,r t H(m)

Debemos mantener en secreto k, y k_f porque estos son los valores que nos permiten demostrar que somos los propietarios del mensaje que vamos a firmar. Los valores H(m), s y r son públicos y los podemos compartir con otros usuarios.

El resultado del proceso de firma es el par de números (r,s) que se pueden utilizar para verificar la firma digital. Este par de número se debe facilitar junto al mensaje, para que los receptores puedan verificar la firma, hay que tener en cuenta que en el proceso se ha utiliza un hash del mensaje, lo que garantiza, que si el mensaje es manipulado, la firma digital no podrá verificarse y por tanto el receptor del mensaje podrá repudiar dicho mensaje.

Algoritmo para verificar la firma.

Una vez que el receptor o receptores, han recibido el mensaje y la firma de este, deben ejecutar este algoritmo para verificar la firma. Los datos necesarios son:

• El mensaje m
• La firma de m que es el par (r,s)
• La clave pública del firmante P_f

Se ejecutan estos pasos:

1. El verificador calcula el hash del mensaje original.
   •  H(m)
2. El verificador calcula:
   • z₁ = H(m)s^-1 (mod n) 
   • z₂ = rs^-1 (mod n)       
3. El verificador calcula:
   • (x,y)= z₁G + z₂P_f
4. La firma es válida si  r = x (mod n) 

En caso de que el número r que el receptor calcula, no coincida con el recibido en la firma, el receptor puede repudiar el mensaje, ya que o ha sido modificado o el firmante no es la identidad que el receptor piensa que es, porque la clave pública utiliza para verificar el mensaje no permite validarlo.

Las curvas

Existen tres curvas elípticas que son las más empleadas actualmente para la firma digital con la tecnología Blockchain. Estas curvas están definidas en el documento “SEC 2: Recommended Elliptic Curve Domain Parameters” (https://www.secg.org/sec2-v2.pdf). En los nombres de las curvas que aparecen en el documento, hay letra en la penúltima posición que es un “k” o una “r”, esta letra indica si la curva es de tipo Koblitz o random.

Las curvas están definidas por un conjunto de parámetros establecidos en la séxtupla:

T = (p, a, b, G, n, h)

• p es un entero que define el orden del cuerpo finito Fp
• a,b ∈ Fp, que definen los coeficientes de la curva elíptica.
• G es un punto base que pertenece a la curva G = (xG, yG) 
• n es un número primo que define el orden de G
• h es un entero el cual cumple h = #E(Fp)/n.

y² = x³ + ax + b

La siguiente tabla muestra una comparación entre las distintas características de varias curvas y el número de bits que debería tener RSA para conseguir la misma fortaleza.

Curva	Fortaleza	Tamaño	RSA/DSA	Koblitz/ random
secp256k1	128	256	3072	k
secp256r1	128	256	3072	r
secp384r1	192	384	7680	r
secp521r1	256	521	15360	r

La fortaleza de una curva es importante, ya que indica la cantidad de trabajo que se necesitaría para romper la curva, es bastante sencillo y se ha explicado en un ejemplo de la sección “El problema a resolver“ en el que se explicaba cuántas operaciones se necesitan de media para acceder a la clave privada. En el ejemplo se exponía que en el caso de utilizar 256 bits, eran necesarias de promedio 2¹²⁸ operaciones, por tanto, la fortaleza es de 128. 

secp256k1 

Es una curva de tipo Koblitz muy utilizada gracias a que es algo más rápida que otras curvas, aunque algo más débil. Esta curva fue creada por Certicom, una compañía canadiense. En el documento “Standards for Efficiency Cryptography (SEC)” puedes encontrar las especificaciones de la curva. Se hizo realmente popular por ser usada en Bitcoin.

Parámetro	Valor
p	0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a	0x0000000000000000000000000000000000000000000000000000000000000000
b	0x0000000000000000000000000000000000000000000000000000000000000007
G	(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
n	0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
h	0x1

a = 0

b = 7

p = 2²⁵⁶-2³²-997

La curva corresponde con la ecuación siguiente:

y² = x³ + 7 (mod p)

prime256v1 

Es una curva desarrollada por NIST, que también recibe el nombre de secp256r1 o P-256. Esta curva es algo más segura que secp256k1, aunque existen ciertas dudas sobre ella, sobre la falta de explicaciones en ciertas constantes, como la semilla que utiliza sobre la que no se han dado explicaciones “c49d360886e704936a6678e1139d26b7819f7e90”. Aunque no significa que sea un problema, la duda está ahí.

Parámetro	Valor
p	0xffffffff00000001000000000000000000000000ffffffffffffffffffffffff
a	0xffffffff00000001000000000000000000000000fffffffffffffffffffffffc
b	0x5ac635d8aa3a93e7b3ebbd55769886bc651d06b0cc53b0f63bce3c3e27d2604b
G	(0x6b17d1f2e12c4247f8bce6e563a440f277037d812deb33a0f4a13945d898c296, 0x4fe342e2fe1a7f9b8ee7eb4a7c0f9e162bce33576b315ececbb6406837bf51f5)
n	0xffffffff00000000ffffffffffffffffbce6faada7179e84f3b9cac2fc632551
h	0x1

p = 2²⁵⁶−2²²⁴+2¹⁹²+2⁹⁶−1

a=−3

b=41058363725152142129326129780047268409114441015993725554835256314039467401291

La curva corresponde con la ecuación siguiente:

y² = x³ -3x + 41058363725152142129326129780047268409114441015993725554835256314039467401291 (mod p)

 secp384r1

Es una curva en la que p es un número primo de 384 bits, también conocida como P-384, esta curva tiene 192 bits de seguridad, mientras que otras curvas tiene 128 bits. 

Parámetro	Valor
p	0xffffffff00000001000000000000000000000000ffffffffffffffffffffffff
a	0xffffffff00000001000000000000000000000000fffffffffffffffffffffffc
b	0xb3312fa7e23ee7e4988e056be3f82d19181d9c6efe8141120314088f5013875ac656398d8a2ed19d2a85c8edd3ec2aef
G	(0xaa87ca22be8b05378eb1c71ef320ad746e1d3b628ba79b9859f741e082542a385502f25dbf55296c3a545e3872760ab7, 0x3617de4a96262c6f5d9e98bf9292dc29f8f41dbd289a147ce9da3113b5f0b8c00a60b1ce1d7e819d7a431d7c90ea0e5f)
n	0xffffffffffffffffffffffffffffffffffffffffffffffffc7634d81f4372ddf581a0db248b0a77aecec196accc52973
h	0x1

p = 2 ³⁸⁴ – 2 ¹²⁸ – 2 ⁹⁶ + 2 ³² – 1

a = -3

b = 27580193559959705877849011840389048093056905856361568521428707301988689241309860865136260764883745107765439761230575

La curva corresponde con la ecuación siguiente:

y² = x³ -3x + 27580193559959705877849011840389048093056905856361568521428707301988689241309860865136260764883745107765439761230575 (mod p)

Conclusión

La criptografía basada en curvas elípticas ha demostrado su utilidad desde que se popularizó en blockchain con Bitcoin, desde entonces, distintas blockchain han empleado estos métodos criptográficos para implementar los procesos de firma digital de transacciones y bloques. Ha demostrado ser una criptografía segura, rápida y que necesita menor número de bits, lo que es una característica esencial, cuando todas las operaciones deben ser firmadas digitalmente.

Existe cierta controversia sobre ciertas curvas, siempre relacionadas con teorías más o menos conspiratorias sobre las curvas NIST, pero la realidad es que se ha demostrado que funcionan, además combinadas con otros métodos de encriptación, como pueden ser métodos simétricos como AES256, permiten implementar modelos de gobernanza sobre los datos gestionados por las soluciones blockchain, más seguros, trazables y resilientes.

El único “pero” que presentan los principales métodos de implementación de criptografía asimétrica, ya que se basan en la dificultad de resolver problemas como la factorización de grandes número, en el caso de RSA, o poder resolver el problema de logaritmos discretos, en el caso de las Curvas Elípticas, es qué pasará con ellos con la llegada de la computación cuántica. Ya que este tipo de computación está avanzando y se espera que en los próximos años esté disponible de manera comercial, es decir, fuera de los laboratorios. La mala noticia es que ya existen algoritmos de computación cuántica que podrían romper RSA y ECC, la buena noticia, es que aún queda tiempo para buscar alternativas e implementar nuevos métodos de criptografía asimétrica. En otro post haremos un repaso sobre las actuales iniciativas relevantes sobre métodos criptográficos post-cuánticos.

José Juan Mora Pérez
CTO & Founder